44 PERFECT SQUARES Part 2

• ODD NUMBERS IN SQUARES
• SQUARES ENDING IN . . .44 AND . . . 444
• PYTHAGOREAN TRIPLES

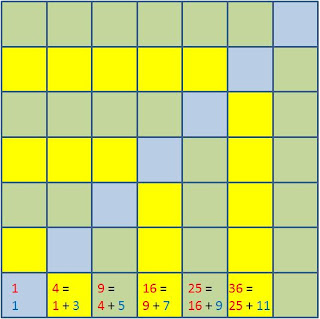
What an odd series the perfect squares make.

0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100

Odd?  Just look at the differences or steps from one to the next.         1,3,5,7,9,11,13,15,17,19

If (n-1) ² is a square, n ² is a square too

and the step from (n-1) ²  to  n²  is the odd number 2n-1

Or using maths; 

n	n2	=	(n-1) 2	+	2n-1
3	9	=	2 x 2	+	5
7	49	=	36	+	13
8	64	=	49	+	15
10	100	=	81	+	19
100	10,000	=	9,801	+	199
101	10201	=	10,000	+	201

Or n^{2              -}                (n-1) ^{2               =                2n-1}

THE PERFECT END FOR A PERFECT SQUARE?

                                                10²   = 100

There is no perfect square below 100 that ends in a repeated numeral.

The next perfect square ending with a repeated numeral is 400.

Did you notice? Yes,  we skipped 144;  12 x 12  =  144

The only nonzero numeral that is repeated to end a perfect square is 4, so:

122	382	622	882	1122	1382	1622	1882	2122	2382
144	1444	3844	7744	12544	19044	26244	35344	44944	56644

In short, the pattern is (50n +/- 12)² = . . . 44

The other thing that caught your eye was 38² with its -444 ending. 

Other -444 endings can be found using (500n +/- 38)²  = . . . 444      

So the set is readily calculated; for a start  

                             (500  +  38 )²   =  (500  +  38 ) x (500  +  38 )   By       FOIL,

                                                =  500 x 500                                        First

     + 2x 500 x38                                  Outside, Inside,

     + 38 x 38                                        Last                

=  250,000       + 38,000  + 1444

                                                =   239,444      

Could this be a party trick?? "Go on, ask me the square of a number between 500 and 540"

When 500 x 500 gives so many zeros, the adding of even biggish numbers gets easy. Since you know a lot of squares already (especially if you know Pythagorean Triples as below), there are probably not many more  to learn. 

  3             4             5

  6             8           10          2[3 - 4 - 5]

  5           12          13

  9           12          15          3[3 - 4 - 5]

  8           15          17

 12          16          20          4[3 - 4 - 5]

  7           24          25

 15          20          25          5[3 - 4 - 5]

 10          24          26          2[5 - 12 - 13]

 20          21          29

 18          24          30          6[3 - 4 - 5]

 16          30          34          2[8 - 15 - 17]

 21          28          35          7[3 - 4 - 5]

 12          35          37

 15          36          39          3[5 - 12 - 13]

 24          32          40          8[3 - 4 - 5]

  9           40          41

Ahh, perfect squares, all 44 of them